「失之毫釐、差之千里」這句古老語錄揭示了測量及空間資訊作業在土木工程中的關鍵性。各工程項目中，即使最細微的測量誤差，也可能導致最後成果出現巨大的誤差。為避免此情況，測量工程人員需謹慎控制可能出現的測量誤差，確保每次測量的準確性，並經由不斷學習與進步，以優化相關工作成果。

當進行測量及空間資訊相關工作時，受到各種因素的影響，導致測量成果出現誤差。例如，利用鋼捲尺多次量測A、B點間距離，每次測量結果可能不一致。同樣，若使用水準儀來測量兩點間的高程差，也會發現返往高程差不會閉合。或者，當我們嘗試用觀測數據來計算一塊土地的面積時，該面積成果也包含從觀測數據中傳播過來的誤差。

在這種情況下，我們需要一種稱為”平差”的方法來改正觀測數據。以一平面四邊形為例，四邊形的內角和為360度，但在實際測量中，觀測數據包含誤差，導致觀測的四個角度和與360度有差異。而平差的目的就是將這些誤差合理地分配到各個觀測數據上，使每個數據都更接近其真實值，從而提高測量的準確性和可靠性。以下將介紹測量誤差與精度、誤差傳播，以及如何進行平差。這些知識對於了解測量及空間資訊有其重要性，並有助於進一步提高測量專業能力。

測量誤差與精度

測量誤差

測量誤差指的是使用儀器測量某個物理量（例如長度、重量、時間等）時，測量之成果與該物理量真值間的差異。在測量學、建築學和其他工程學領域，此概念極為重要。想像要測量一張桌子的長度，若使用一把年久失修而磨損的老式皮捲尺，那所得之測量成果必有所偏差。以土木工程為例，工程師利用「水準儀」測量地表兩點之高度差時，若水準儀沒有完全正確校正，造成水準氣泡偏離中心，而導致系統性誤差，這意味著每次使用此儀器進行測量時，會得到一個與真值有相同程度的偏差。

另一例子是，工程師常使用「全測站」來測量工地的角度和距離，若於風大時操作，狂風可能會導致儀器輕微晃動，進而產生隨機誤差，這種誤差是不可預測的，使得每次的測量結果都會呈現隨機變動。在進行測量作業時，清楚了解並考慮這些潛在誤差極其重要，故工程師需要定期校正儀器，選擇適當的測量條件和環境，並使用高精度的設備，以降低測量誤差並獲得更可靠的數據，這對於確保工程安全與成功是至關重要。

而什麼叫真值? 真值是指一個物理量的確切或實際值。在測量學中，真值是一個理想化的概念，通常無法直接取得，但它是所有測量作業的參考標準。我們通常透過測量作業來接近或估算出真值。舉例來說，若你參加一場測量比賽，任務是測量學校的操場面積，理論上，操場面積有一確切數值，即為「真值」。但於實際測量時，無論是使用測距儀、經緯儀或其他工具，所獲得的測量成果都可能與真值有所偏差，而這種偏差源於多種因素，例如儀器的不精確、改正不完全，或風吹動了儀器等。在此情況下，操場面積真值無法直接取得，然而，測量員可透過多次觀測後取平均值，或者使用更精準的測量工具，來讓成果更接近真值。

在工程領域，接近真值是一項重要的追求，因為這能確保我們得到的數據和成果的準確性。透過了解可能產生的測量誤差並採取相對應的措施來消除或減低它們，我們可以使得測量結果更接近真值，從而提升我們的工作可靠度和效益。

 

測量誤差由多種原因產生，以下三個為常見來源：

儀器誤差：因測量儀器本身的不完善所導致，例如，水準尺存在微小刻度誤差。此外，若測量儀器沒有正確校正，也可能產生誤差。儀器校正是確保測量工作準確性的關鍵步驟，若無適當的校正，測量成果可能與真值存在較大差異。

人為誤差：人的操作技巧和觀察能力也可能導致測量誤差。比如，使用不正確的測量方法、讀數時的視覺判斷有誤、或操作上的細微差異，都可能產生誤差。

自然環境影響：環境條件的變化也可能對測量結果產生影響。例如，溫度、濕度、氣壓等因素的變化，可能會改變儀器的性能或測量物體的特性，從而產生誤差。

這些測量誤差並非測量員的錯誤，而是在測量過程中無法避免的現象。我們應該盡可能消除或減低這些誤差，但也應認識到測量誤差的存在，並在分析和解釋資料時，進行適當的改正。透過正確記錄和評估測量誤差，能有效提升測量可靠度，求得更精確的成果。

 

測量誤差主要可以區分為以下三種：

粗差: 通常源於人為的疏忽或操作錯誤。這些誤差並非像其他誤差類型可被預測或系統化，而是偶然發生的。例如，當使用皮捲尺測量距離時，若皮捲尺未正確對齊點位，或在讀取皮捲尺時看錯刻度，這些都可能產生粗差。粗差的特性通常很明顯，並且與其他測量值有顯著差異。

隨機誤差：於測量過程中的偶然因素引起的，它無法預測且無法消除，此誤差在多次重複測量中可能產生不同的讀數。隨機誤差是由各種隨機因素造成的，例如人反應時間的微小變化、環境條件的微小變動或測量儀器讀數的微小波動。隨機誤差通常是在測量成果的不確定性範圍內出現的，例如，假設你使用一個溫度計測量室內溫度，儘管方法和儀器是一樣的，但每次測量成果都有微小變化，如23.1°C,、23.2°C、 23.0°C等，這些微小差異即是隨機誤差。

系統誤差：是指測量中因儀器或方法之缺陷而系統性地偏離真值的誤差。這種誤差在多次觀測中是一致的，通常具有相同的方向和大小，與隨機誤差不同，系統誤差不是偶然出現，是可被預測和改正。例如，使用鋼捲尺量測時，每次都比真值小0.5 厘米，那麼測量結果將永遠低估實際值。系統性誤差通常是由儀器的不準確性、測量方法的缺陷或操作技巧上的錯誤所引起的，了解並偵測出系統誤差對於測量成果的準確性是很重要的，一旦知道系統誤差的來源和大小，就可以通過校正儀器或使用數學模型來修正，從而得到更接近真值的測量成果。

瞭解這三種誤差的特性相當重要。粗差會導致最後測量成果完全錯誤，系統性誤差會導致測量結果偏離真值，而隨機誤差則會在多次的測量中產生隨機變化。工程測量人員可透過校正儀器、改進測量方法和提高操作技巧來減少系統性誤差；而隨機誤差雖無法完全消除，但可透過多次重複觀測後取平均值來降低其影響；粗差則可透過增進操作技巧、多次觀測偵測等方式移除。下圖為粗差、隨機誤差與系統誤差示意圖：

測量精度

「精度」是一科學和工程領域中常用的術語，有助於描述測量成果的品質。於討論精度時，通常會提到「準確度(Accuracy)」和「精密度(Precision)」這兩個相關概念。

準確度 (Accuracy)：描述測量成果與真值之接近程度。例如使用電子測距儀量測兩點間距離，當觀測值與實際長度相當接近，那可說測量是準確的，若儀器沒有精確校正，那麼測量成果可能會偏離真值，那測量工作就不夠準確。

精密度 (Precision)：描述重複觀測同一個物理量時，這些測量值間的一致性或相似性。例如使用一鋼捲尺多次測量實際距離10公尺之A、B兩點，若每次皆觀測得非常相近之讀數（如10.03公尺、10.04公尺、10.02公尺），即使這些讀數不一定非常接近10公尺，我們仍可說這個距離量測具有良好的精密度。

現在，讓我們用一個更容易理解的範例來加深理解。想像軍人正在打靶，準確度代表射出的箭是否接近靶心，若非常接近靶心，那麼你的射擊就很準確。而精密度代表射出的箭是否彼此靠近，若彼此非常靠近，即使不在靶心附近，那你的射擊就具有高精密度。下圖依序呈現高準確度與高精密度、高準確度與低精密度、低準確度與低精密度、低準確度與高精密度，最後的圖呈現粗差。

 

準確度 (Accuracy)的表示方式：

均方根誤差 (Root Mean Square Error, RMSE):描述觀測值與真值之間的差異，當均方根誤差越大，準確度越低。

均方根誤差可由下式計算:

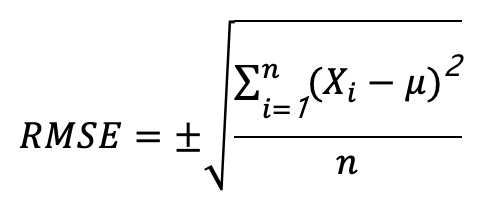
Σ : “求和”，就是把一系列數字加起來
X_i : 每一個數據值
μ: 平均值
n : 觀測量的數量

一個簡單例子: 假設學者正在進行一氣溫預測模型研究，其將預測值與實際溫度進行比較。以下分別為五天內預測和觀測溫度：

第1天：預測溫度 20度，實際溫度 22度

第2天：預測溫度 25度，實際溫度 26度

第3天：預測溫度 23度，實際溫度 23度

第4天：預測溫度 27度，實際溫度 25度

第5天：預測溫度 22度，實際溫度 23度

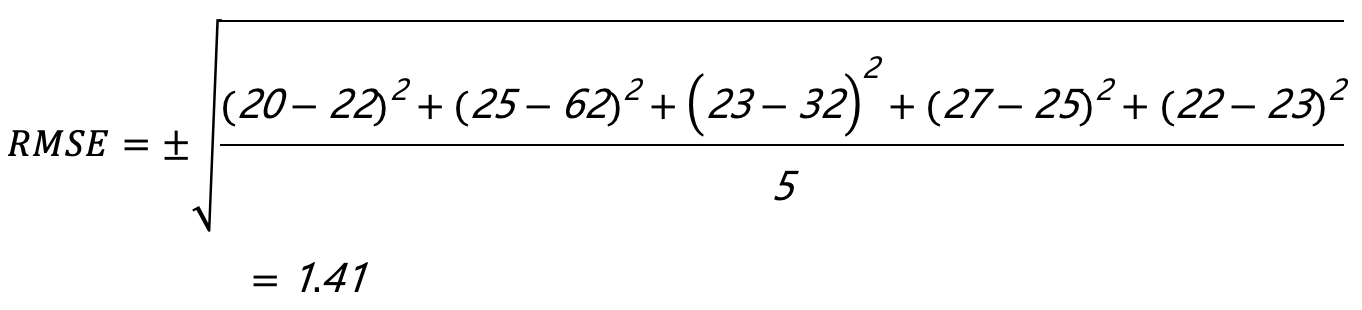
這意味模型預測溫度之均方根誤差為1.41度。均方根誤差可用於衡量預測模型準確度的指標，均方根誤差越小，表示模型預測準確度越高。

 

精密度 (precision)的表示方式(包含但不限於)：

1. 標準偏差(Standard deviation，SD): 用來衡量資料的分散程度，告訴我們資料與平均值間的差異大小。標準偏差越大，資料分散程度越大，精密度越低；標準偏差越小，資料越集中，精密度越高。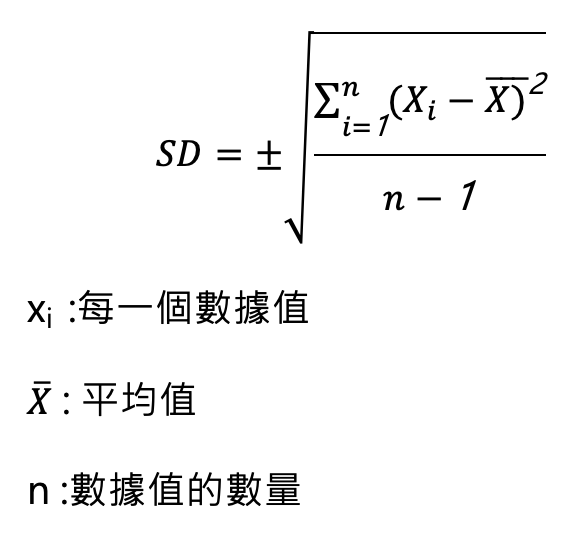

利用一簡單例子來解釋。假設我們有五個朋友，他們的年齡分別是 10, 12, 13, 15, 和 18 歲，那如何計算他們年齡的標準偏差。

首先，計算平均年齡：(10 + 12 + 13 + 15 + 18) / 5 = 13.6

接著，用每個年齡減去平均年齡，然後將結果平方：(10-13.6)², (12-13.6)², (13-13.6)², (15-13.6)², (18-13.6)²

把這些平方相加，然後除以年齡數量：[(10-13.6)² + (12-13.6)² + (13-13.6)² + (15-13.6)² + (18-13.6)²] / 5

最後，取平方根：

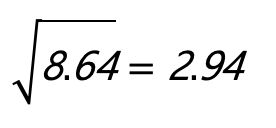
所以，這五個朋友年齡的標準偏差是 2.94 歲。

2.平均誤差(Average Error, AE): 偶然誤差e_i絕對值的期望值，是一種衡量預測或測量值與實際值之間差異的方法。

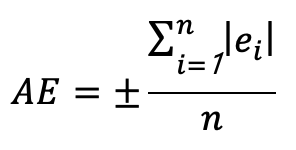
e_i :每一個誤差值，計算方式是預測值減去實際值 (預測值 – 實際值)

n :偶然誤差的數量

利用一個簡單例子來解釋。假設你是一位科學老師，學生正在做測量工作，測量一橡皮球從不同高度掉落的時間。學生先預測掉落時間，然後實際測量它。數據如下：

高度(cm)	預測時間(sec)	實際時間(sec)
50	0.5	0.6
100	0.9	1.0
150	1.3	1.5

 

首先，計算每個高度的誤差：e1 = 0.5 – 0.6 = -0.1, e2 = 0.9 – 1.0 = -0.1, e3 = 1.3 – 1.5 = -0.2

然後，把這些誤差的絕對值相加： 0.1 + (0.1) + (0.2) = 0.4

最後，除以數據的數量：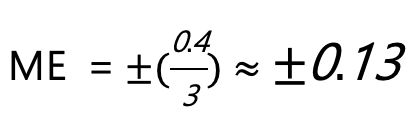 

所以，學生的預測的平均誤差大約是 ±0.13 秒。

3.或然誤差(Probable Error): 在一些特定的情況下，或然誤差可能被視為特定統計數據範圍內的一種誤差估計。在這種情況下，或然誤差可表示成:

或然誤差 (PE) =± c x SD

SD :樣本的標準偏差

c: 一個特定的數學常數，它來自於常態分佈的性質；c=0.67、1、1.96或3分別代表約占標準常態分佈的50%、68%、95%、99.7%。

假設一樣本之標準偏差為2，50%或然誤差是:

PE = 0.67x 2 =± 1.34

這意味測量值有50%的機率落在真值的±1.34的範圍內。或然誤差提供了一種有關測量值精密度的簡單估計。然而，此估計方法並不適用於所有情況，尤其資料不符合常態分佈時。

4.相對精度(relative error): 一種衡量測量成果精密度的方法，它比較了測量誤差與量測值本身的大小。換句話說，相對精度描述了量測誤差與測量結果之間的比例關係。

相對精度的計算公式如下：

相對精度 = （絕對誤差 / 量測值） x 100%

舉一例子來更清楚地解釋這個概念：假設正在量測一段距離，量測結果是20公尺。然而，這段距離的真實距離是21公尺。在此情況下，絕對誤差為1公尺（21 – 20），而相對精度計算如下：

相對精度 = （1 / 20） x 100% = 5%

這意味著測量結果比真實距離小5%。這個數字顯示此次量測之誤差與量測值間的比例是多少，相對精度值越低，表示測量精密度越高。

誤差傳播

測量工程人員可透過各種方式來收集空間資訊資料，例如水準測量觀測高程差、經緯儀觀測角度、電子測距儀觀測距離等。一般來說，若粗差和系統誤差已消除，任何形式之量測方式都存在觀測偶然誤差，對後續資料的應用皆產生影響。比如我們要利用上述的觀測量來計算坐標或面積等，觀測誤差就會傳播到面積或坐標計算成果上。

用一個簡單範例來說明線性誤差傳播。假設正在進行工程測量，測量員需要量測兩段道路的距離，然後將這兩段距離相加來計算總距離。測距儀量測出之第一段路距離為20±0.10公尺，第二段路距離為30±0.10公尺。所以，兩段路的總距離為 D = 20 m + 30 m = 50 m，而總距離的中誤差 = 

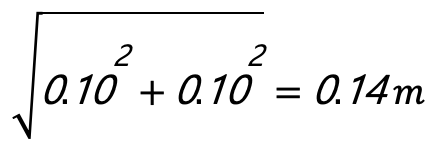
所以兩段路的總距離為50公尺 ± 0.14公尺。這就是如何使用誤差傳播來估計成果的不確定性。

將上述的誤差傳播廣義地概念化，並用矩陣的形式表示。在現實生活上，很多的量測都是非線性的，例如長方形面積的量測。假設觀測量Ｘ與最或是值Ｙ有著函數關係，即

Y=F(X)

其中Y為因變數向量，X為觀測變數向量：

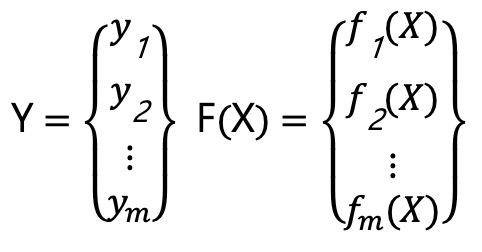
這裡有m個因變數。因Y與F(X)為非線性關係，我們必須將其非線性關係轉變成線性關係，使之能滿足誤差傳播的準則。從非線性關係變成線性關係，稱之為線性化，即

Y=A(X)

其中

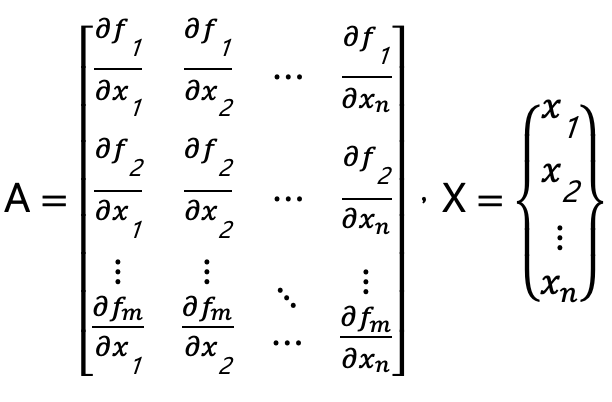
這裡有n個觀測變數，A則為線性化之後的係數矩陣。因此Y標準偏差 可被表示為

其中

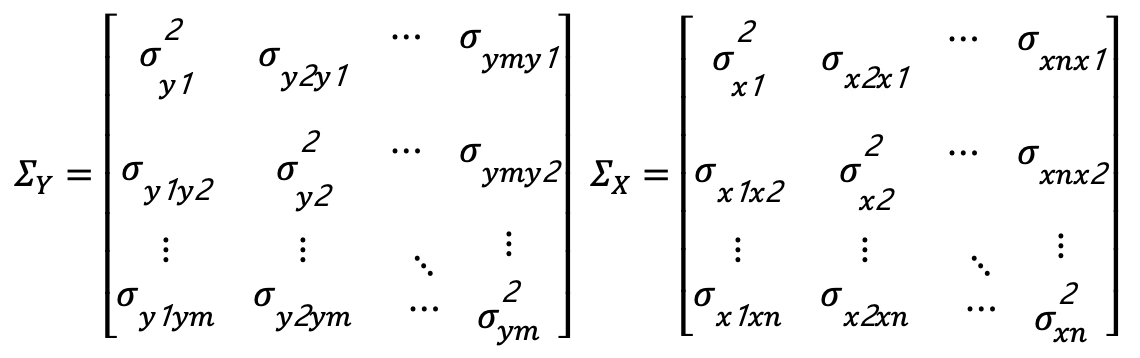
這裡提共一範例:

假設長方形邊長及標準偏差分別為

以及

，且Ｘ和Ｙ獨立不相關，那長方形面積標準偏差為何？

長方形面積Ｆ=XY，面積Ｆ與Ｘ和Ｙ兩變數有著函數關係。因此，我們必須將此關係線性化：

步驟一：計算係數矩陣

步驟二：建構觀測變異數矩陣

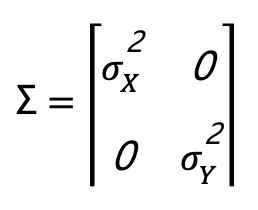
步驟三：長方形面積標準偏差為

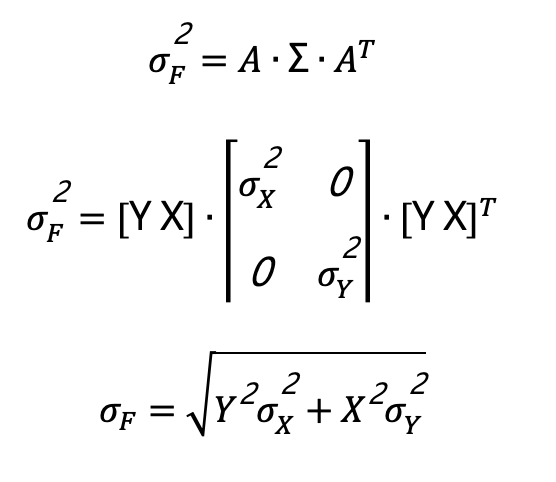
平差概論

在測量學中，平差是一種統計方法，用於分析和處理觀測數據以改善其精度。它的主要目的是找出觀測數據中的隨機誤差，並糾正這些誤差以得到更精確的結果。平差的主要原則是基於「最小平方」法則，也就是說，調整觀測值以使誤差平方和達到最小。這意味著透過數學方法，平差可以找出最接近所有測量結果的最佳數值。利用一簡單例子來解釋。假設你正使用皮捲尺量測一個房間的長度，重複量測了五次結果：4.0公尺、4.1公尺、3.9公尺、4.0公尺和3.8公尺。你可以直接取這五個結果的平均值，但這樣可能會忽略了每次量測的微小誤差。透過平差，你可以更詳細地處理這些數據。在這個例子中，平差可能包括將每次測量的結果和平均值進行比較，計算每次測量的偏差，然後將這些偏差平方並加總，然後找出可以使這個總數最小的測量值。這個測量值將被視為最接近實際長度的數值。在這個過程中，你可能發現一些觀測數據和其他數據相差很大，這可能是因為在測量過程中出現了偶然誤差。這些偶然誤差在平差過程中會被識別出來，並從最終結果中去除。

 

平差的主要任務即是處理觀測值之間的誤差，並依據觀測量與最優化模式之間的關係，利用所有的觀測數據進行的最佳估值計算，並評定觀測以及估算精度。這裡觀測量與最優化模式之間的關係，指的是找出觀測量的特性，已建立符合觀測模式的機制。

舉例來說，在測量中，如果施測一段距離，其觀測值為 ，

其每次觀測的權重分別為

，則加權平均最或是值為：

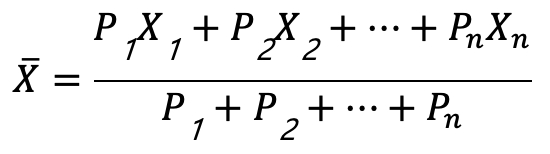
其中，觀測先驗權重可以由每個觀測值的標準偏差建構而成，即

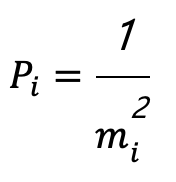
而觀測後驗的標準偏差即為

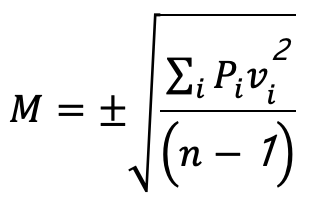
而最或是值的標準偏差為

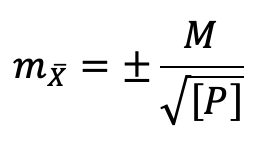
來一個數值例題:

同一距離施測十天，得到每一天平均值以及標準偏差如下，試求該距離的最或是值及其標準偏差？

天	平均值 （單位公尺）	標準差（單位公尺）
1	800.62	0.01
2	800.63	0.02
3	800.64	0.04
4	800.63	0.04
5	800.65	0.04
6	800.60	0.02
7	800.61	0.02
8	800.60	0.04
9	800.61	0.01
10	800.60	0.02

距離最或是值為:

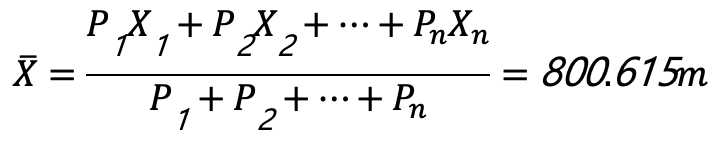
其中權重為標準偏差平方倒數分之一，即

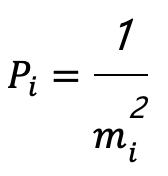
誤差向量

因此後驗單位權中誤差和估值中誤差為

 

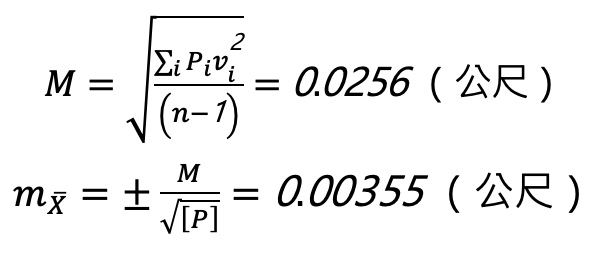
此答案為平差之後的結果。我們主要是利用所收集過來的觀測數據，透過平差的過程找到一個最佳解，該解在 情況下，其值為最小所估算而得。